集成学习【一】

集成学习

• 集成学习 (ensemble learning) 是通过构建及结合多个学习器来完成学习任务的，其一般结构为：

  • 先产生一组个体学习器 (individual learner)。个体学习器通常由一种或多种现有的学习算法从训练数据中产生

  • 然后使用某种 strategy 将个体学习器结合起来。通常可以获得比单一学习器显著优越的泛化性能

• 选取基学习器的准则：好而不同

  • 个体学习器要具备一定的准确性，预测能力不能太差

  • 个体学习器之间要有差异

• 一个简单的理论分析：

  考虑一个二分类问题 $y\in -1, +1$，真实函数 $f(x)$ 及奇数 $M$ 个相互独立的犯错概率为 $\epsilon$ 的个体学习器 $h_i(x)$，我们使用简单的投票 (voting) 规则进行决策：

  $$H(x)=sign(\sum_{i=1}^{M}h_i(x))$$

  由 $Hoeffding$ 不等式可知，集成学习的犯错概率满足：

  $$P(H(x) \not = f(x)) = \sum_{k=1}^{(M+1)/2}C_{M}^{k}(1-\epsilon)^k\epsilon^{M-k} \le exp{(-\frac{1}{2}M(1-2\epsilon)^2)}$$

  当基学习器的个数 $M$ 很大的时候，集成学习的犯错概率将接近于 $0$。这也很符合人们的直觉：大多数人同时犯错的概率将很低。

• 根据基学习器的生成方式，目前的集成学习方法大概分成两类：

  • 个体学习器之间存在强依赖关系，必须串行生成的序列化方法，每一轮迭代生成一个个体学习器，其中以 Boosting 为代表
  • 个体学习器之间不存在强依赖关系， 可以同时生成的并行化方法，其中以 Bagging 和 Random Forest 为代表

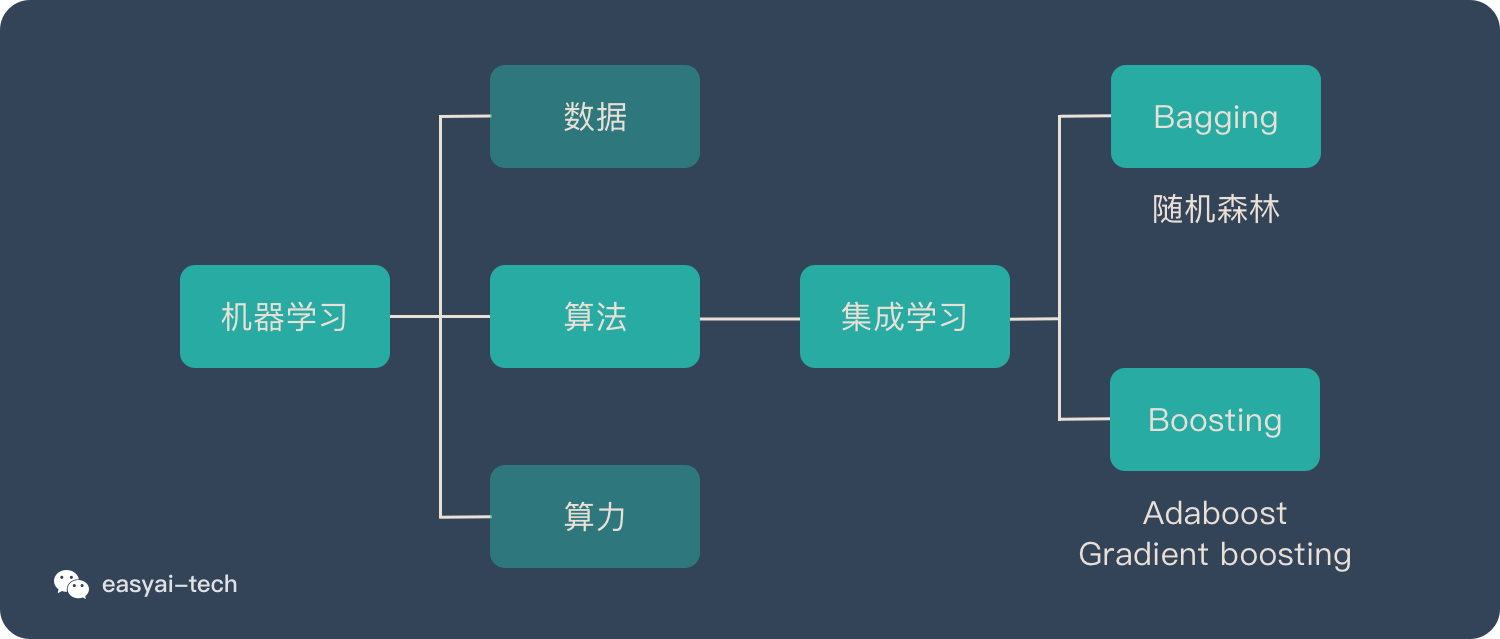
集成学习归属于机器学习，他是一种 训练思路，并不是某种具体的方法或者算法。

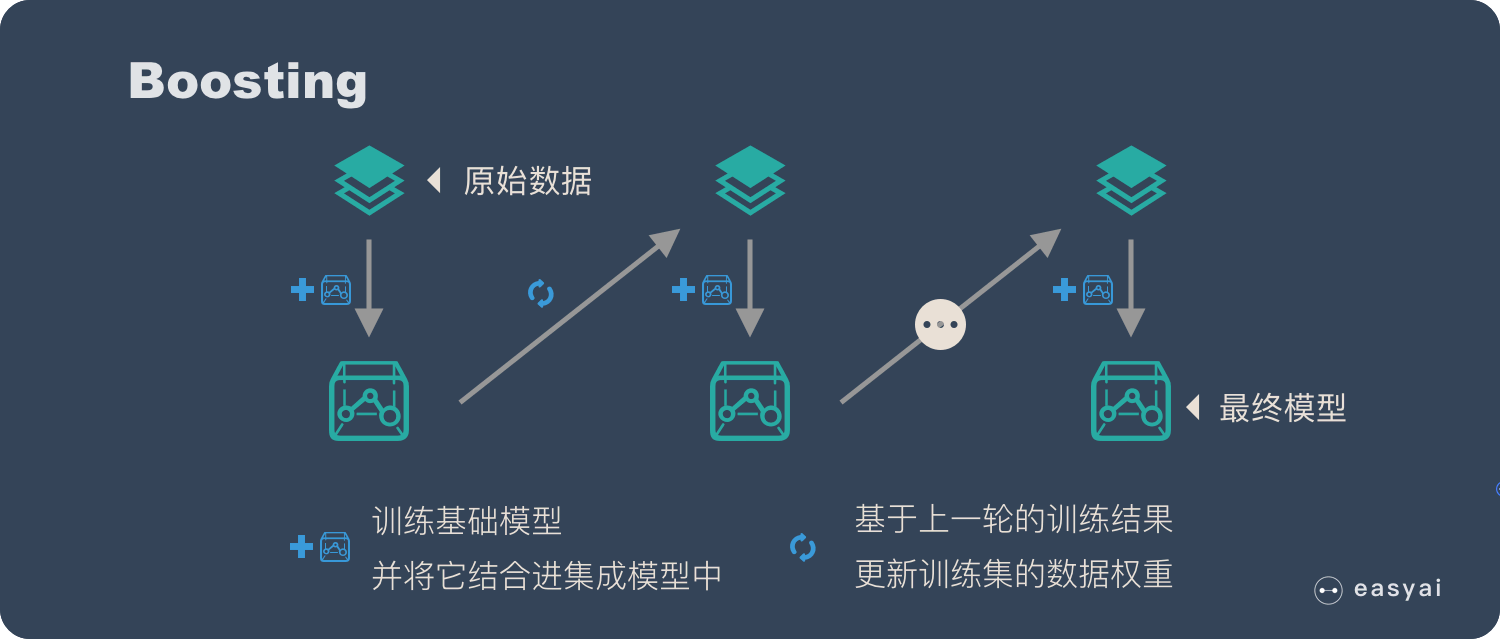
Boosting

Boosting 的主要思想是将弱的基学习器提升为强学习器，在分类问题中，它通过改变训练样本的权重学习多个分类器，并将这些分类器们进行线性组合来提高分类的能力。其主要步骤为：

• 先用样本权重相等的训练集学习一个初始的基学习器

• 根据上一轮得到的学习器在训练集上的表现情况调整样本权重（提高被上一轮学习器分类错误的样本的权重，使之再下一轮训练中得到更多关注），然后据此学习一个新的基学习器

• 重复第二步直到得到$M$个学习器，最后的集成学习器为$M$个学习器的组合

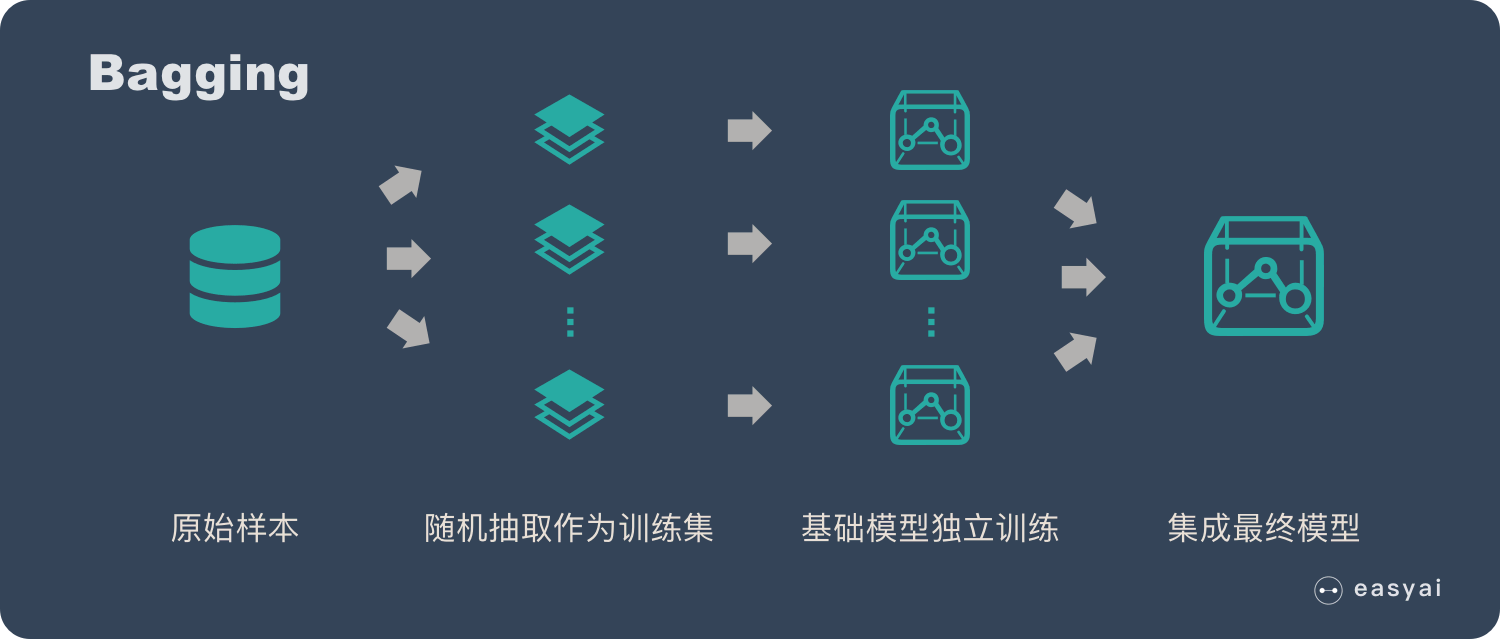
Bagging

Bagging 直接基于自主采样 Boostrap Sampling。自主采样的一般步骤为：

• 先随机取出一个样本放入采样集中，再把该样本放回原始数据集。

• 这样经过$N$次随机采样操作，得到包含$N$个样本的采样集。

初始训练集中有的样本在采样集中多次出现，有的则从未出现。初始训练集中约有 $63.2\%$ 的样本出现在了采样集中。因此剩下的约 $36.8\%$ 的样本可用作验证集来对泛化性能进行包外估计。

Bagging方法的主要步骤为：

• 经过 $M$ 轮自助采样，可以得到 $M$ 个包含 $N$ 个训练样本的采样集。

• 然后基于每个采样集训练出一个基学习器。

• 最后将这$M$个基学习器进行组合，得到集成模型。

偏差-方差分解

$$Error = bias + var_f + var_{\epsilon}$$

即泛化误差可以分解为偏差、方差和噪声之和：

偏差：度量了学习算法的期望预测与真实结果之间的偏离程度，刻画了学习算法本身的拟合能力。

方差：度量了训练集的变动所导致的学习性能的变化，刻画了数据扰动造成的影响。

噪声：度量了在当前任务上任何学习算法所能达到的期望泛化误差的下界，刻画了学习问题本身的难度。

偏差-方差分解表明：泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度共同决定的。

在 Bagging 和 Boosting 框架中，通过计算基模型的期望和方差我们可以得到模型整体的期望和方差。为了简化模型，我们假设基模型的期望为 $\mu$ ，方差 $\sigma^2$ ，模型的权重为 $r$，两两模型间的相关系数 $\rho$ 相等。由于 Bagging 和 Boosting 的基模型都是线性组成的，那么有：

$$F=\sum_{i}^m r_if_i$$ $$E(F) = \sum_{i}^m r_iE(f_i)$$ $$var(F) = var(\sum_{i}^m r_if_i)$$

对于 Bagging 来说，每个基模型的权重等于 $1/m$ 且期望近似相等。

• 整体模型的期望等于基模型的期望，这也就意味着整体模型的偏差和基模型的偏差近似。

• 整体模型的方差小于等于基模型的方差，随着基模型数量增多，整体模型的方差减少，从而防止过拟合的能力增强，模型的准确度得到提高。

• 因此 Bagging 中的基模型一定要为强模型。

对于 Boosting 来说，由于基模型共用同一套训练集，所以基模型间具有强相关性，因此整体模型的方差近似等于基模型的方差。

• Bagging 主要关注降低方差，它能平滑强学习器的方差。因此它在非剪枝决策树、神经网络等容易受到样本扰动的学习器上效果更为明显。

• Boosting 主要关注降低偏差，它能将一些弱学习器提升为强学习器。因此它在 SVM、KNN 等不容易受到样本扰动的学习器上效果更为明显。